Topological Sort
June 3, 2021
Introduction
A topological sort of a directed acyclic graph (DAG) is a linear ordering of all the nodes of the graph such that a comes before b if the edge a->b exists in the DAG. A DAG will always have one or possibly more topologically sorted orderings.
Figure1: Directed Acyclic Graph
Consider the DAG above. One possible topological sort for this DAG is: A, B, C, D, E, F, G, H, I. Observe that for any pair of characters (p1, p2) in ordering (A, B, C, D, E, F, G, H, I) p1 comes before p2.
In a typical technical interview you will most likely encounter a question that asks you to determine whether a topological ordering is possible for a graph rather than generating the ordering itself. Furthermore, the graph will not be given to you as a variable, you'll need to infer that the problem is a topological sort problem by paying close attention to the problem description.
An Example
**There are a total of N courses you have to take, labeled from 0 to N - 1. You are given an array prerequisites where prereq[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai. For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1. Return true if you can finish all courses. Otherwise, return false.
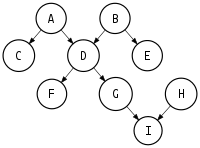 Figure1:Â Directed Acyclic Graph
Figure1:Â Directed Acyclic Graph
The key to solving this problem is to understand that prerequisites cannot be cyclic. For example if course A is a prereq to course B and course B is a prereq to course C then course C cannot be a prereq to course A otherwise we have a cycle and we would not be able to take any of the courses.
This problem can be modeled as a directed acyclic graph where the courses, 0, 1, 2, ..., N-1 are the nodes in the graph and an edge exists from a -> b iff a is a prerequisite of b.
For our case, the way our input is given [ai, bi] indicates that course bi must be taken before course ai so we need to be careful and make sure that we have bi -> ai in the graph we construct.
Algorithm & Code
- construct a directed graph using the prerequisites array (may be cyclic or acylic. we don't know yet)
- we determine all the in degrees for each node and store them in an array
- we loop through our array and store all our 0 degree nodes in a queue
- while our queue is not empty we remove the front element and for all neighbors of the node we decrease their in degree
- the above action simulates the removal of the node and all its corresponding edges from the graph
- if there are neighbor nodes with an in degree of 0 we place them in the queue
- while we do this we keep track of how many nodes we have processed
- at the end of this operation if we haven't processed all nodes, then there must be a cycle in the graph

Topological Sort (Kahn's Algorithm)
The above algorithm where we remove nodes and decrease in-degrees is called Kahn's algorithm. There is also a way to determine whether a we can topologically sort a directed graph using a depth first first approach. The key idea is to have two arrays, one which determines if a node has been visited, and another which determines whether a node is in a current dfs path.
Then for each unvisited node we perform dfs. If on entry we find that the node is on the current dfs path, that means we just encountered a cycle and the graph is not a directly acyclic graph. If on the other hand if the node is not on the current path, but has been visited before then we can confidently return true to the question of whether the graph is acyclic because a previous dfs search has already told us the graph is acyclic. Then if we get past both these checks, we mark both visted and on current path to true and perform dfs on the neighbors of the node. If at any point we find a cyclic path we stop the loop and return early. Otherwise we reset to onCurrentPath to false and return true. The code follows below.

Topological Sort using Depth First Search
Note if we actually wanted to track the linear ordering, all we have to do is add an additional parameter for a list that can track the nodes as we enter the dfs. Then at the end of every successful acyclic path, we push the node to the list. It's important to make sure though to reverse the list at the end of the process because we will be visiting the most "dependent" node at the very end. Also the onCurrentPath check should precede the visited check in this scenario because only when a node IS NOT on a current path but is visited can we be sure that it's acyclic.
Practice Problems
MEDIUM
HARD